- Essentials
- Getting Started
- Agent
- API
- APM Tracing
- Containers
- Dashboards
- Database Monitoring
- Datadog
- Datadog Site
- DevSecOps
- Incident Management
- Integrations
- Internal Developer Portal
- Logs
- Monitors
- OpenTelemetry
- Profiler
- Session Replay
- Security
- Serverless for AWS Lambda
- Software Delivery
- Synthetic Monitoring and Testing
- Tags
- Workflow Automation
- Learning Center
- Support
- Glossary
- Standard Attributes
- Guides
- Agent
- Integrations
- Developers
- Authorization
- DogStatsD
- Custom Checks
- Integrations
- Create an Agent-based Integration
- Create an API Integration
- Create a Log Pipeline
- Integration Assets Reference
- Build a Marketplace Offering
- Create a Tile
- Create an Integration Dashboard
- Create a Monitor Template
- Create a Cloud SIEM Detection Rule
- OAuth for Integrations
- Install Agent Integration Developer Tool
- Service Checks
- IDE Plugins
- Community
- Guides
- OpenTelemetry
- Administrator's Guide
- API
- Partners
- Datadog Mobile App
- DDSQL Reference
- CoScreen
- CoTerm
- Cloudcraft (Standalone)
- In The App
- Dashboards
- Notebooks
- DDSQL Editor
- Reference Tables
- Sheets
- Monitors and Alerting
- Metrics
- Watchdog
- Bits AI
- Internal Developer Portal
- Error Tracking
- Change Tracking
- Service Management
- Actions & Remediations
- Infrastructure
- Cloudcraft
- Resource Catalog
- Universal Service Monitoring
- Hosts
- Containers
- Processes
- Serverless
- Network Monitoring
- Cloud Cost
- Application Performance
- APM
- APM Terms and Concepts
- Application Instrumentation
- APM Metrics Collection
- Trace Pipeline Configuration
- Correlate Traces with Other Telemetry
- Trace Explorer
- Recommendations
- Code Origins for Spans
- Service Observability
- Endpoint Observability
- Dynamic Instrumentation
- Live Debugger
- Error Tracking
- Data Security
- Guides
- Troubleshooting
- Continuous Profiler
- Database Monitoring
- Agent Integration Overhead
- Setup Architectures
- Setting Up Postgres
- Setting Up MySQL
- Setting Up SQL Server
- Setting Up Oracle
- Setting Up Amazon DocumentDB
- Setting Up MongoDB
- Connecting DBM and Traces
- Data Collected
- Exploring Database Hosts
- Exploring Query Metrics
- Exploring Query Samples
- Exploring Database Schemas
- Exploring Recommendations
- Troubleshooting
- Guides
- Data Streams Monitoring
- Data Jobs Monitoring
- Data Observability
- Digital Experience
- Real User Monitoring
- Synthetic Testing and Monitoring
- Continuous Testing
- Product Analytics
- Software Delivery
- CI Visibility
- CD Visibility
- Deployment Gates
- Test Optimization
- Quality Gates
- DORA Metrics
- Security
- Security Overview
- Cloud SIEM
- Code Security
- Cloud Security
- App and API Protection
- Workload Protection
- Sensitive Data Scanner
- AI Observability
- Log Management
- Observability Pipelines
- Log Management
- Administration
Outlier Monitor
Overview
Outlier detection is an algorithmic feature that allows you to detect when a specific group is behaving different compared to its peers. For example, you could detect that one web server in a pool is processing an unusual number of requests, or significantly more 500 errors are happening in one AWS availability zone than the others.
Monitor creation
To create an outlier monitor in Datadog, navigate to Monitors > New Monitor > Outlier.
Define the metric
Any metric currently reporting to Datadog is available for monitors. For more information, see the Metric Monitor page.
The outlier monitor requires a metric with a group (hosts, availability zones, partitions, etc.) that has three or more members, which exhibit uniform behavior.
Set alert conditions
- Trigger a separate alert for each outlier
<GROUP> - during the last
5 minutes,15 minutes,1 hour, and so on, or usecustomto set a value between 1 minute and 1 year. - Using algorithm
MAD,DBSCAN,scaledMAD, orscaledDBSCAN - tolerance:
0.33,1.0,3.0, etc. - %:
10,20,30, etc. (only forMADalgorithms)
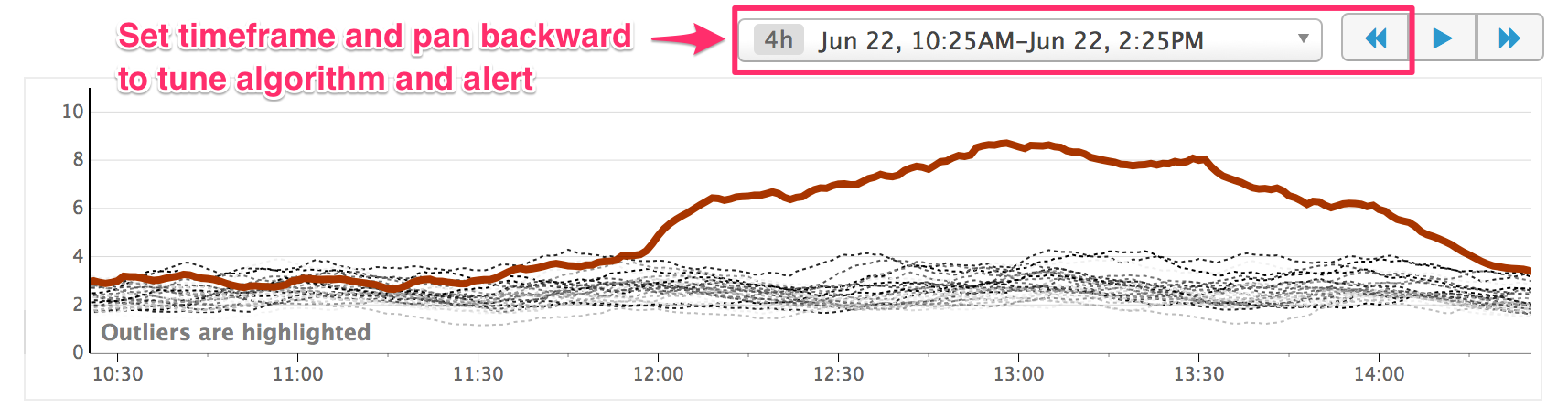
When setting up an outlier monitor, the time window is an important consideration. If the time window is too large, you might not be alerted in time. If the time window is too short, the alerts are not as resilient to one-off spikes.
To ensure your alert is properly calibrated, set the time window in the preview graph and use the reverse («) button to look back in time at outliers that would have triggered an alert. Additionally, you can use this feature to tune your parameters to a specific outlier algorithm.
Algorithms
Datadog offers two types of outlier detection algorithms: DBSCAN/scaledDBSCAN and MAD/scaledMAD. It is recommended to use the default algorithm, DBSCAN. If you have trouble detecting the correct outliers, adjust the parameters of DBSCAN or try the MAD algorithm. The scaled algorithms may be useful if your metrics are large scale and closely clustered.
DBSCAN (density-based spatial clustering of applications with noise) is a popular clustering algorithm. Traditionally, DBSCAN takes:
- A parameter
𝜀that specifies a distance threshold under which two points are considered to be close. - The minimum number of points that have to be within a point’s
𝜀-radiusbefore that point can start agglomerating.
Datadog uses a simplified form of DBSCAN to detect outliers on timeseries. Each group is considered to be a point in d-dimensions, where d is the number of elements in the timeseries. Any point can agglomerate, and any point not in the largest cluster is considered an outlier. The initial distance threshold is set by creating a new median timeseries by taking the median of the values from the existing timeseries at every time point. The Euclidean distance between each group and the median series is calculated. The threshold is set as the median of these distances, multiplied by a normalizing constant.
Parameters
This implementation of DBSCAN takes one parameter, tolerance, the constant by which the initial threshold is multiplied to yield DBSCAN’s distance parameter 𝜀. Set the tolerance parameter according to how similarly you expect your groups to behave—larger values allow for more tolerance in how much a group can deviate from its peers.
MAD (median absolute deviation) is a robust measure of variability, and can be viewed as the robust analog for standard deviation. Robust statistics describe data in a way that is not influenced by outliers.
Parameters
To use MAD for your outlier monitor, configure the parameters tolerance and %.
Tolerance specifies the number of deviations a point (independently of the groups) needs to be away from the median for it to be considered an outlier. This parameter should be tuned depending on the expected variability of the data. For example, if the data is generally within a small range of values, then this should be small. Otherwise, if points can vary greatly, then set a higher scale so the variabilities do not trigger false positives.
Percent refers to the percentage of points in the group considered as outliers. If this percentage is exceeded, the whole group is marked as an outlier.
DBSCAN and MAD have scaled versions (scaledDBSCAN and scaledMAD). In most situations, the scaled algorithms behave the same as their regular counterparts. However, if DBSCAN/MAD algorithms are identifying outliers within a closely clustered group of metrics, and you would like the outlier detection algorithm to scale with the overall magnitude of the metrics, try the scaled algorithms.
DBSCAN vs. MAD
So which algorithm should you use? For most outliers, any algorithm performs well at the default settings. However, there are subtle cases where one algorithm is more appropriate.
In the following image, a group of hosts is flushing their buffers together, while one host is flushing its buffer slightly later. DBSCAN picks this up as an outlier whereas MAD does not. This is a case where you might prefer to use MAD since the synchronization of the group is just an artifact of the hosts being restarted at the same time. On the other hand, if instead of flushed buffers, the metrics represented a scheduled job that should be synchronized across hosts, DBSCAN would be the correct choice.
Advanced alert conditions
For detailed instructions on the advanced alert options (auto resolve, new group delay, etc.), see the Monitor configuration page.
Notifications
For detailed instructions on the Configure notifications and automations section, see the Notifications page.
API
To create outlier monitors programmatically, see the Datadog API reference. Datadog recommends exporting a monitor’s JSON to build the query for the API.
Troubleshooting
The outlier algorithms are set up to identify groups that are behaving differently from their peers. If your groups exhibit “banding” behavior as shown below (maybe each band represents a different shard), Datadog recommends tagging each band with an identifier, and setting up outlier detection alerts on each band separately.
Further Reading
Additional helpful documentation, links, and articles: