- Essentials
- Getting Started
- Agent
- API
- APM Tracing
- Containers
- Dashboards
- Database Monitoring
- Datadog
- Datadog Site
- DevSecOps
- Incident Management
- Integrations
- Internal Developer Portal
- Logs
- Monitors
- OpenTelemetry
- Profiler
- Session Replay
- Security
- Serverless for AWS Lambda
- Software Delivery
- Synthetic Monitoring and Testing
- Tags
- Workflow Automation
- Learning Center
- Support
- Glossary
- Standard Attributes
- Guides
- Agent
- Integrations
- Developers
- Authorization
- DogStatsD
- Custom Checks
- Integrations
- Create an Agent-based Integration
- Create an API Integration
- Create a Log Pipeline
- Integration Assets Reference
- Build a Marketplace Offering
- Create a Tile
- Create an Integration Dashboard
- Create a Monitor Template
- Create a Cloud SIEM Detection Rule
- OAuth for Integrations
- Install Agent Integration Developer Tool
- Service Checks
- IDE Plugins
- Community
- Guides
- OpenTelemetry
- Administrator's Guide
- API
- Partners
- Datadog Mobile App
- DDSQL Reference
- CoScreen
- CoTerm
- Cloudcraft (Standalone)
- In The App
- Dashboards
- Notebooks
- DDSQL Editor
- Reference Tables
- Sheets
- Monitors and Alerting
- Metrics
- Watchdog
- Bits AI
- Internal Developer Portal
- Error Tracking
- Change Tracking
- Service Management
- Actions & Remediations
- Infrastructure
- Cloudcraft
- Resource Catalog
- Universal Service Monitoring
- Hosts
- Containers
- Processes
- Serverless
- Network Monitoring
- Cloud Cost
- Application Performance
- APM
- APM Terms and Concepts
- Application Instrumentation
- APM Metrics Collection
- Trace Pipeline Configuration
- Correlate Traces with Other Telemetry
- Trace Explorer
- Recommendations
- Code Origins for Spans
- Service Observability
- Endpoint Observability
- Dynamic Instrumentation
- Live Debugger
- Error Tracking
- Data Security
- Guides
- Troubleshooting
- Continuous Profiler
- Database Monitoring
- Agent Integration Overhead
- Setup Architectures
- Setting Up Postgres
- Setting Up MySQL
- Setting Up SQL Server
- Setting Up Oracle
- Setting Up Amazon DocumentDB
- Setting Up MongoDB
- Connecting DBM and Traces
- Data Collected
- Exploring Database Hosts
- Exploring Query Metrics
- Exploring Query Samples
- Exploring Database Schemas
- Exploring Recommendations
- Troubleshooting
- Guides
- Data Streams Monitoring
- Data Jobs Monitoring
- Data Observability
- Digital Experience
- Real User Monitoring
- Synthetic Testing and Monitoring
- Continuous Testing
- Product Analytics
- Software Delivery
- CI Visibility
- CD Visibility
- Deployment Gates
- Test Optimization
- Quality Gates
- DORA Metrics
- Security
- Security Overview
- Cloud SIEM
- Code Security
- Cloud Security
- App and API Protection
- Workload Protection
- Sensitive Data Scanner
- AI Observability
- Log Management
- Observability Pipelines
- Log Management
- Administration
Anomaly Monitor
Overview
Anomaly detection is an algorithmic feature that identifies when a metric is behaving differently than it has in the past, taking into account trends, seasonal day-of-week, and time-of-day patterns. It is suited for metrics with strong trends and recurring patterns that are hard to monitor with threshold-based alerting.
For example, anomaly detection can help you discover when your web traffic is unusually low on a weekday afternoon—even though that same level of traffic is normal later in the evening. Or consider a metric measuring the number of logins to your steadily-growing site. Because the number increases daily, any threshold would be outdated, whereas anomaly detection can alert you if there is an unexpected drop—potentially indicating an issue with the login system.
Monitor creation
To create an anomaly monitor in Datadog, use the main navigation: Monitors –> New Monitor –> Anomaly.
Define the metric
Any metric reporting to Datadog is available for monitors. For more information, see the Metric Monitor page.
Note: The anomalies function uses the past to predict what is expected in the future, so using it on a new metric may yield poor results.
After defining the metric, the anomaly detection monitor provides two preview graphs in the editor:
- The Historical View allows you to explore the monitored query at different time scales to better understand why data may be considered anomalous or non-anomalous.
- The Evaluation Preview is longer than the alerting window and provides insight on what the anomalies algorithm takes into account when calculating the bounds.
Set alert conditions
Trigger an alert if the values have been above or below, above, or below the bounds for the last 15 minutes, 1 hour, etc. or custom to set a value between 15 minutes and 2 weeks. Recover if the values are within the bounds for at least 15 minutes, 1 hour, etc. or custom to set a value between 15 minutes and 2 weeks.
- Anomaly detection
- With the default option (
above or below) a metric is considered to be anomalous if it is outside of the gray anomaly band. Optionally, you can specify whether being onlyaboveorbelowthe bands is considered anomalous. - Trigger window
- How much time is required for the metric to be anomalous before the alert triggers. Note: If the alert window is too short, you might get false alarms due to spurious noise.
- Recovery window
- The amount of time required for the metric to no longer be considered anomalous, allowing the alert to recover. It is recommended to set the Recovery Window to the same value as the Trigger Window.
Note: The range of accepted values for the Recovery Window depends on the Trigger Window and the Alert Threshold to ensure the monitor can’t both satisfy the recovery and the alert condition at the same time. Example:
Threshold: 50%Trigger window: 4h The range of accepted values for the recovery window is between 121 minutes (4h*(1-0.5) +1 min = 121 minutes) and 4 hours. Setting a recovery window below 121 minutes could lead to a 4 hour timeframe with both 50% of anomalous points and the last 120 minutes with no anomalous points.
Another example:
Threshold: 80%Trigger window: 4h The range of accepted values for the recovery window is between 49 minutes (4h*(1-0.8) +1 min = 49 minutes) and 4 hours.
Advanced options
Datadog automatically analyzes your chosen metric and sets several parameters for you. However, the options are available for you to edit under Advanced Options.
- Deviations
- The width of the gray band. This is equivalent to the bounds parameter used in the anomalies function.
- Algorithm
- The anomaly detection algorithm (
basic,agile, orrobust). - Seasonality
- The seasonality (
hourly,daily, orweekly) of the cycle for theagileorrobustalgorithm to analyze the metric. - Daylight savings
- Available for
agileorrobustanomaly detection withweeklyordailyseasonality. For more information, see Anomaly Detection and Time Zones. - Rollup
- The rollup interval.
- Thresholds
- The percentage of points that need to be anomalous for alerting, warning, and recovery.
Seasonality
- Hourly
- The algorithm expects the same minute after the hour behaves like past minutes after the hour, for example 5:15 behaves like 4:15, 3:15, etc.
- Daily
- The algorithm expects the same time today behaves like past days, for example 5pm today behaves like 5pm yesterday.
- Weekly
- The algorithm expects that a given day of the week behaves like past days of the week, for example this Tuesday behaves like past Tuesdays.
Required data history for Anomaly Detection algorithm: Machine learning algorithms require at least three time as much historical data time as the chosen seasonality time to compute the baseline. For example:
- weekly seasonality requires at least three weeks of data
- daily seasonality requires at least three days of data
- hourly seasonality requires at least three hours of data
All of the seasonal algorithms may use up to six weeks of historical data when calculating a metric’s expected normal range of behavior. By using a significant amount of past data, the algorithms avoid giving too much weight to abnormal behavior that might have occurred in the recent past.
Anomaly detection algorithms
- Basic
- Use when metrics have no repeating seasonal pattern. Basic uses a simple lagging rolling quantile computation to determine the range of expected values. It uses little data and adjusts quickly to changing conditions but has no knowledge of seasonal behavior or longer trends.
- Agile
- Use when metrics are seasonal and expected to shift. The algorithm quickly adjusts to metric level shifts. A robust version of the SARIMA algorithm, it incorporates the immediate past into its predictions, allowing quick updates for level shifts at the expense of being less robust to recent, long-lasting anomalies.
- Robust
- Use when seasonal metrics expected to be stable, and slow, level shifts are considered anomalies. A seasonal-trend decomposition algorithm, it is stable and predictions remain constant even through long-lasting anomalies at the expense of taking longer to respond to intended level shifts (for example, if the level of a metric shifts due to a code change.)
Examples
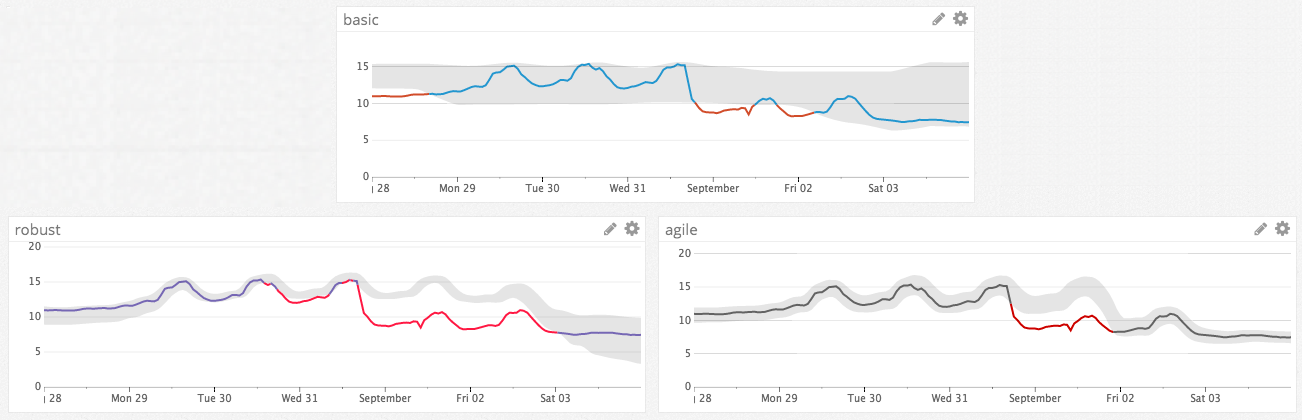
The graphs below illustrate how and when these three algorithms behave differently from one another.
Anomaly detection comparison for hourly seasonality
In this example, basic successfully identifies anomalies that spike out of the normal range of values, but it does not incorporate the repeating, seasonal pattern into its predicted range of values. By contrast, robust and agile both recognize the seasonal pattern and can detect more nuanced anomalies, for example if the metric was to flat-line near its minimum value. The trend also shows an hourly pattern, so the hourly seasonality works best in this case.
Anomaly detection comparison for weekly seasonality
In this example, the metric exhibits a sudden level shift. Agile adjusts more quickly to the level shift than robust. Also, the width of robust’s bounds increases to reflect greater uncertainty after the level shift; the width of agile’s bounds remains unchanged. Basic is clearly a poor fit for this scenario, where the metric exhibits a strong weekly seasonal pattern.
Comparison of algorithm reactions to change
This example shows how the algorithms react to an hour-long anomaly. Robust does not adjust the bounds for the anomaly in this scenario since it reacts more slowly to abrupt changes. The other algorithms start to behave as if the anomaly is the new normal. Agile even identifies the metric’s return to its original level as an anomaly.
Comparison of algorithm reactions to scale
The algorithms deal with scale differently. Basic and robust are scale-insensitive, while agile is not. The graphs on the left below show agile and robust mark the level-shift as being anomalous. On the right, 1000 is added to the same metric, and agile no longer calls out the level-shift as being anomalous whereas robust continues do so.
Anomaly detection comparison for new metrics
This example shows how each algorithm handles a new metric. Robust and agile does not show any bounds during the first few seasons (weekly). Basic starts showing bounds shortly after the metric first appears.
Advanced alert conditions
For detailed instructions on the advanced alert options (auto resolve, evaluation delay, etc.), see the Monitor configuration page. For the metric-specific option full data window, see the Metric monitor page.
Notifications
For detailed instructions on the Configure notifications and automations section, see the Notifications page.
API
Customers on an enterprise plan can create anomaly detection monitors using the create-monitor API endpoint. Datadog strongly recommends exporting a monitor’s JSON to build the query for the API. By using the monitor creation page in Datadog, customers benefit from the preview graph and automatic parameter tuning to help avoid a poorly configured monitor.
Note: Anomaly detection monitors are only available to customers on an enterprise plan. Customers on a pro plan interested in anomaly detection monitors should reach out to their customer success representative or email the Datadog billing team.
Anomaly monitors are managed using the same API as other monitors. These fields are unique for anomaly monitors:
query
The query property in the request body should contain a query string in the following format:
avg(<query_window>):anomalies(<metric_query>, '<algorithm>', <deviations>, direction='<direction>', alert_window='<alert_window>', interval=<interval>, count_default_zero='<count_default_zero>' [, seasonality='<seasonality>']) >= <threshold>
query_window- A timeframe like
last_4horlast_7d. The time window displayed in graphs in notifications. Must be at least as large as thealert_windowand is recommended to be around 5 times thealert_window. metric_query- A standard Datadog metric query (for example,
sum:trace.flask.request.hits{service:web-app}.as_count()). algorithmbasic,agile, orrobust.deviations- A positive number; controls the sensitivity of the anomaly detection.
direction- The directionality of anomalies that should trigger an alert:
above,below, orboth. alert_window- The timeframe to be checked for anomalies (for example,
last_5m,last_1h). interval- A positive integer representing the number of seconds in the rollup interval. It should be smaller or equal to a fifth of the
alert_windowduration. count_default_zero- Use
truefor most monitors. Set tofalseonly if submitting a count metric in which the lack of a value should not be interpreted as a zero. seasonalityhourly,daily, orweekly. Exclude this parameter when using thebasicalgorithm.threshold- A positive number no larger than 1. The fraction of points in the
alert_windowthat must be anomalous in order for a critical alert to trigger.
Below is an example query for an anomaly detection monitor, which alerts when the average Cassandra node’s CPU is three standard deviations above the ordinary value over the last 5 minutes:
avg(last_1h):anomalies(avg:system.cpu.system{name:cassandra}, 'basic', 3, direction='above', alert_window='last_5m', interval=20, count_default_zero='true') >= 1
options
Most of the properties under options in the request body are the same as for other query alerts, except for thresholds and threshold_windows.
thresholds- Anomaly monitors support
critical,critical_recovery,warning, andwarning_recoverythresholds. Thresholds are expressed as numbers from 0 to 1, and are interpreted as the fraction of the associated window that is anomalous. For example, acriticalthreshold value of0.9means that a critical alert triggers when at least 90% of the points in thetrigger_window(described below) are anomalous. Or, awarning_recoveryvalue of 0 means that the monitor recovers from the warning state only when 0% of the points in therecovery_windoware anomalous. - The
criticalthresholdshould match thethresholdused in thequery. threshold_windows- Anomaly monitors have a
threshold_windowsproperty inoptions.threshold_windowsmust include both two properties—trigger_windowandrecovery_window. These windows are expressed as timeframe strings, such aslast_10morlast_1h. Thetrigger_windowmust match thealert_windowfrom thequery. Thetrigger_windowis the time range which is analyzed for anomalies when evaluating whether a monitor should trigger. Therecovery_windowis the time range that analyzed for anomalies when evaluating whether a triggered monitor should recover.
A standard configuration of thresholds and threshold window looks like:
"options": {
...
"thresholds": {
"critical": 1,
"critical_recovery": 0
},
"threshold_windows": {
"trigger_window": "last_30m",
"recovery_window": "last_30m"
}
}
Troubleshooting
Further Reading
Additional helpful documentation, links, and articles: