- Essentials
- Getting Started
- Agent
- API
- APM Tracing
- Containers
- Dashboards
- Database Monitoring
- Datadog
- Datadog Site
- DevSecOps
- Incident Management
- Integrations
- Internal Developer Portal
- Logs
- Monitors
- OpenTelemetry
- Profiler
- Session Replay
- Security
- Serverless for AWS Lambda
- Software Delivery
- Synthetic Monitoring and Testing
- Tags
- Workflow Automation
- Learning Center
- Support
- Glossary
- Standard Attributes
- Guides
- Agent
- Integrations
- Developers
- Authorization
- DogStatsD
- Custom Checks
- Integrations
- Create an Agent-based Integration
- Create an API Integration
- Create a Log Pipeline
- Integration Assets Reference
- Build a Marketplace Offering
- Create a Tile
- Create an Integration Dashboard
- Create a Monitor Template
- Create a Cloud SIEM Detection Rule
- OAuth for Integrations
- Install Agent Integration Developer Tool
- Service Checks
- IDE Plugins
- Community
- Guides
- OpenTelemetry
- Administrator's Guide
- API
- Partners
- Datadog Mobile App
- DDSQL Reference
- CoScreen
- CoTerm
- Cloudcraft (Standalone)
- In The App
- Dashboards
- Notebooks
- DDSQL Editor
- Reference Tables
- Sheets
- Monitors and Alerting
- Metrics
- Watchdog
- Bits AI
- Internal Developer Portal
- Error Tracking
- Change Tracking
- Service Management
- Actions & Remediations
- Infrastructure
- Cloudcraft
- Resource Catalog
- Universal Service Monitoring
- Hosts
- Containers
- Processes
- Serverless
- Network Monitoring
- Cloud Cost
- Application Performance
- APM
- APM Terms and Concepts
- Application Instrumentation
- APM Metrics Collection
- Trace Pipeline Configuration
- Correlate Traces with Other Telemetry
- Trace Explorer
- Recommendations
- Code Origins for Spans
- Service Observability
- Endpoint Observability
- Dynamic Instrumentation
- Live Debugger
- Error Tracking
- Data Security
- Guides
- Troubleshooting
- Continuous Profiler
- Database Monitoring
- Agent Integration Overhead
- Setup Architectures
- Setting Up Postgres
- Setting Up MySQL
- Setting Up SQL Server
- Setting Up Oracle
- Setting Up Amazon DocumentDB
- Setting Up MongoDB
- Connecting DBM and Traces
- Data Collected
- Exploring Database Hosts
- Exploring Query Metrics
- Exploring Query Samples
- Exploring Database Schemas
- Exploring Recommendations
- Troubleshooting
- Guides
- Data Streams Monitoring
- Data Jobs Monitoring
- Data Observability
- Digital Experience
- Real User Monitoring
- Synthetic Testing and Monitoring
- Continuous Testing
- Product Analytics
- Software Delivery
- CI Visibility
- CD Visibility
- Deployment Gates
- Test Optimization
- Quality Gates
- DORA Metrics
- Security
- Security Overview
- Cloud SIEM
- Code Security
- Cloud Security
- App and API Protection
- Workload Protection
- Sensitive Data Scanner
- AI Observability
- Log Management
- Observability Pipelines
- Log Management
- Administration
Smoothing
Autosmooth
| Function | Description | Example |
|---|---|---|
autosmooth() | Automatically removes noise while preserving the trend of the metric. | autosmooth(<METRIC_NAME>{*}) |
The autosmooth() function applies a moving average with an automatically selected span. It smooths a timeseries while preserving its trend. In this example, the function chooses the optimal span to smooth the timeseries:
When used on a group by query, such as avg by, the same span is applied on all the timeseries. If used on several metrics in the same graph, different spans can be selected to optimally smooth each one of the metric timeseries.
The algorithm is inspired by the ASAP algorithm-you can read more about it in this blog post.
The autosmooth() function cannot be used in monitors. Being that the span is chosen dynamically, the result of applying the function could change from minute to minute, making threshold setting difficult and leading to alert flapping.
Exponentially weighted moving average
Ewma 3
| Function | Description | Example |
|---|---|---|
ewma_3() | Compute the exponentially weighted moving average over a span of 3. | ewma_3(<METRIC_NAME>{*}) |
Note: The span value is twice the weighted average age of the series. So ewma_3() is comparable to a 3-day rolling average.
Example:
If a metric 10 + x%10 {*} increments itself by 1 starting from 10 until it drops back to 10 after 10 data points, then ewma3(10 + x%10 {*}) has the following shape:
Ewma 5
| Function | Description | Example |
|---|---|---|
ewma_5() | Compute the exponentially weighted moving average over a span of 5. | ewma_5(<METRIC_NAME>{*}) |
Note: The span value is twice the weighted average age of the series. So ewma_5() is comparable to a 5-day rolling average.
Example:
If a metric 10 + x%10 {*} increments itself by 1 starting from 10 until it drops back to 10 after 10 data points, then ewma5(10 + x%10 {*}) has the following shape:
Ewma 7
| Function | Description | Example |
|---|---|---|
ewma_7() | Compute the exponentially weighted moving average over a span of 7. | ewma_7(<METRIC_NAME>{*}) |
Note: The span value is twice the weighted average age of the series. So ewma_7() is comparable to a 7-day rolling average.
Ewma 10
| Function | Description | Example |
|---|---|---|
ewma_10() | Compute the exponentially weighted moving average over a span of 10. | ewma_10(<METRIC_NAME>{*}) |
Note: The span value is twice the weighted average age of the series. So ewma_10() is comparable to a 10-day rolling average.
Example:
If a metric 10 + x%10 {*} increments itself by 1 starting from 10 until it drops back to 10 after 10 data points, then ewma10(10 + x%10 {*}) has the following shape:
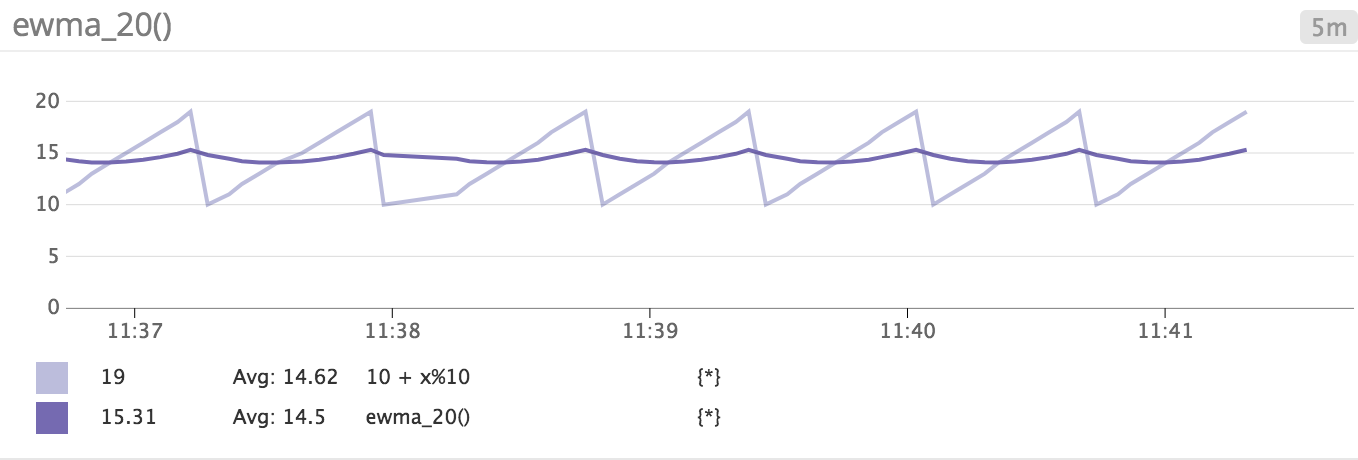
Ewma 20
| Function | Description | Example |
|---|---|---|
ewma_20() | Compute the exponentially weighted moving average over a span of 20. | ewma_20(<METRIC_NAME>{*}) |
Note: The span value is twice the weighted average age of the series. So ewma_20() is comparable to a 20-day rolling average.
Example:
If a metric 10 + x%10 {*} increments itself by 1 starting from 10 until it drops back to 10 after 10 data points, then ewma20(10 + x%10 {*}) has the following shape:
Median
Median 3
| Function | Description | Example |
|---|---|---|
median_3() | Rolling median with a span of 3. | median_3(<METRIC_NAME>{*}) |
Note: The span value is the number of data points. So median_3() uses the last 3 data points to calculate the median.
Median 5
| Function | Description | Example |
|---|---|---|
median_5() | Rolling median with a span of 5. | median_5(<METRIC_NAME>{*}) |
Note: The span value is the number of data points. So median_5() uses the last 5 data points to calculate the median.
Median 7
| Function | Description | Example |
|---|---|---|
median_7() | Rolling median with a span of 7. | median_7(<METRIC_NAME>{*}) |
Note: The span value is the number of data points. So median_7() uses the last 7 data points to calculate the median.
Median 9
| Function | Description | Example |
|---|---|---|
median_9() | Rolling median with a span of 9. | median_9(<METRIC_NAME>{*}) |
Note: The span value is the number of data points. So median_9() uses the last 9 data points to calculate the median.
Weighted
Weighted() is only available when querying `SUM BY` on gauge type metrics.
| Function | Description | Example |
|---|---|---|
weighted() | Automatically removes noise while preserving the proper weight of transient tags. | sum:(<GAUGE_METRIC_NAME>{*}).weighted() |
The weighted() function accounts for the short-lived lifespan of transient, churning tag values when summing gauge metrics in space to prevent artificial spikes.
This function is automatically appended to queries on gauge metrics if both of the following conditions are met:
- The metric has a regular, consistent submission interval that is also specified on Metrics Summary
- The metric is aggregated with
SUM by(for example,sum: mygaugemetric{*})
Here is an example graph of the original query with inaccurate spikes (in purple) and the query with the properly weighted calculation (in green):
For more information on the weighted() modifier, see How does weighted() work?.
Other functions
Consult the other available functions:
- Algorithmic: Implement Anomaly or Outlier detection on your metric.