- Principales informations
- Getting Started
- Agent
- API
- Tracing
- Conteneurs
- Dashboards
- Database Monitoring
- Datadog
- Site Datadog
- DevSecOps
- Incident Management
- Intégrations
- Internal Developer Portal
- Logs
- Monitors
- OpenTelemetry
- Profileur
- Session Replay
- Security
- Serverless for AWS Lambda
- Software Delivery
- Surveillance Synthetic
- Tags
- Workflow Automation
- Learning Center
- Support
- Glossary
- Standard Attributes
- Guides
- Agent
- Intégrations
- Développeurs
- OpenTelemetry
- Administrator's Guide
- API
- Partners
- Application mobile
- DDSQL Reference
- CoScreen
- CoTerm
- Remote Configuration
- Cloudcraft
- In The App
- Dashboards
- Notebooks
- DDSQL Editor
- Reference Tables
- Sheets
- Alertes
- Watchdog
- Métriques
- Bits AI
- Internal Developer Portal
- Error Tracking
- Change Tracking
- Service Management
- Actions & Remediations
- Infrastructure
- Cloudcraft
- Resource Catalog
- Universal Service Monitoring
- Hosts
- Conteneurs
- Processes
- Sans serveur
- Surveillance réseau
- Cloud Cost
- Application Performance
- APM
- Termes et concepts de l'APM
- Sending Traces to Datadog
- APM Metrics Collection
- Trace Pipeline Configuration
- Connect Traces with Other Telemetry
- Trace Explorer
- Recommendations
- Code Origin for Spans
- Observabilité des services
- Endpoint Observability
- Dynamic Instrumentation
- Live Debugger
- Suivi des erreurs
- Sécurité des données
- Guides
- Dépannage
- Profileur en continu
- Database Monitoring
- Agent Integration Overhead
- Setup Architectures
- Configuration de Postgres
- Configuration de MySQL
- Configuration de SQL Server
- Setting Up Oracle
- Setting Up Amazon DocumentDB
- Setting Up MongoDB
- Connecting DBM and Traces
- Données collectées
- Exploring Database Hosts
- Explorer les métriques de requête
- Explorer des échantillons de requêtes
- Exploring Database Schemas
- Exploring Recommendations
- Dépannage
- Guides
- Data Streams Monitoring
- Data Jobs Monitoring
- Data Observability
- Digital Experience
- RUM et Session Replay
- Surveillance Synthetic
- Continuous Testing
- Product Analytics
- Software Delivery
- CI Visibility
- CD Visibility
- Deployment Gates
- Test Visibility
- Code Coverage
- Quality Gates
- DORA Metrics
- Feature Flags
- Securité
- Security Overview
- Cloud SIEM
- Code Security
- Cloud Security Management
- Application Security Management
- Workload Protection
- Sensitive Data Scanner
- AI Observability
- Log Management
- Pipelines d'observabilité
- Log Management
- CloudPrem
- Administration
Comprendre la fonction de rollup et la cardinalité dans les visualisations
Section Overview
Les visualisations dans l’analyse de données reposent souvent sur des fonctions d’agrégation pour résumer les données au fil du temps. Un défi courant survient lorsque la fonction de rollup et les mesures de cardinalité distincte ou unique interagissent entre elles, entraînant des résultats inattendus lors de la visualisation des données.
En alignant les attentes avec la nature des résultats de rollup et en utilisant des requêtes claires, vous pouvez obtenir des informations précieuses à partir de vos données. Ce document explique comment fonctionne la fonction de rollup, en particulier dans le contexte de la cardinalité, et fournit des pratiques recommandées sur la façon d’interpréter les résultats de visualisation avec précision.
Comprendre la cardinalité dans les séries temporelles
Considérez un scénario où vous suivez les utilisateurs visitant un site web. Chaque jour pendant sept jours, vous observez 100 utilisateurs, ce qui vous amène à supposer un total de 700 utilisateurs. Cependant, le nombre réel d’utilisateurs uniques au cours de la semaine peut être de 400, car de nombreux utilisateurs visitent le site plusieurs jours. Cette divergence survient parce que chaque plage temporelle (comme chaque jour) compte indépendamment les utilisateurs uniques, gonflant le total par rapport à une seule plage temporelle de rollup plus longue.
Ce résultat contre-intuitif est dû à la cardinalité, qui fait référence à la façon dont les éléments uniques dans un ensemble de données sont comptés. La cardinalité pour chaque bucket temporel peut être complexe. Lors de l’analyse des utilisateurs, considérez la question : “Combien d’utilisateurs uniques ont visité le site chaque jour cette semaine ?” Si un utilisateur visite le site deux jours distincts, il compte comme unique pour chaque jour.
Comment le rollup affecte les moyennes
La fonction de rollup impacte également de manière significative la façon dont les moyennes sont calculées et affichées dans les visualisations :
Effet de lissage :
- Les périodes plus courtes (rollups de 5 minutes) montrent des pics et des variations plus détaillés.
- Les périodes plus longues (rollups de 30 minutes) créent des graphiques plus lisses.
Calculs de moyenne :
- Dans les périodes plus courtes, les moyennes peuvent être plus faibles car Datadog ne capture que les utilisateurs à ce moment précis.
- Dans les périodes plus longues, les moyennes peuvent être plus élevées car Datadog capture plus d’instances d’utilisateurs utilisant différents appareils.
Exemple : comment le rollup affecte les comptages d’utilisateurs uniques
Les visualisations affichent la somme des valeurs sur différents intervalles, ce qui peut créer une confusion lors de la comparaison des totaux sur différentes périodes. Par exemple, un graphique peut afficher des totaux différents pour la même métrique lorsqu’il est consulté à différentes échelles de temps (comme des intervalles de 5 minutes par rapport à 30 minutes). Cette différence se produit parce que les utilisateurs peuvent être comptés plusieurs fois dans des fenêtres temporelles plus courtes, mais une seule fois dans des fenêtres temporelles plus longues.
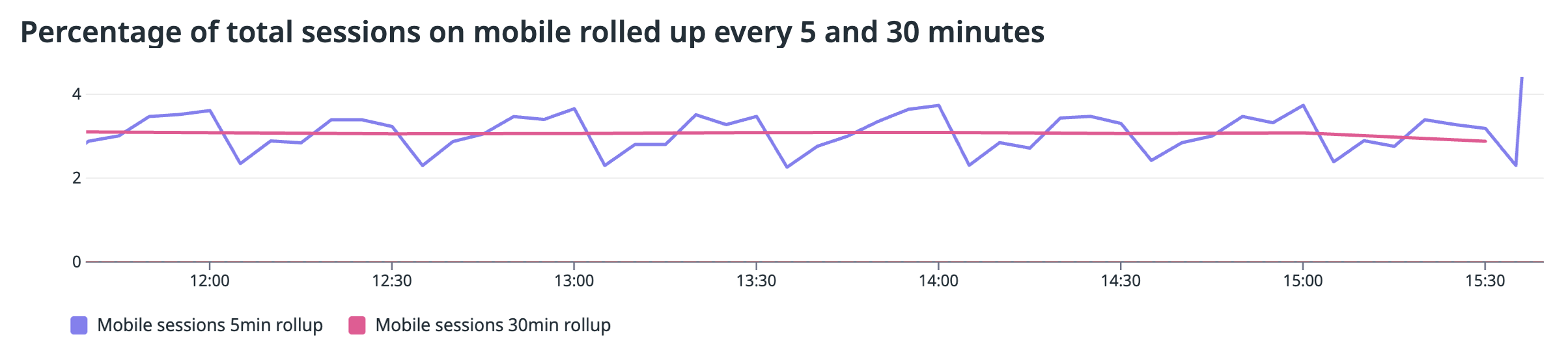
Cette section présente un exemple qui démontre comment les fonctions de rollup et la cardinalité interagissent dans la pratique. Considérez un site web qui suit les sessions utilisateur sur mobile et desktop.
Lorsque vous prenez une moyenne des sessions sur mobile et que vous effectuez un rollup toutes les 30 minutes, vous obtenez une version lissée du graphique. Cet effet de lissage est un résultat naturel de la fonction de rollup, rendant la visualisation plus facile à interpréter pour les tendances à long terme.
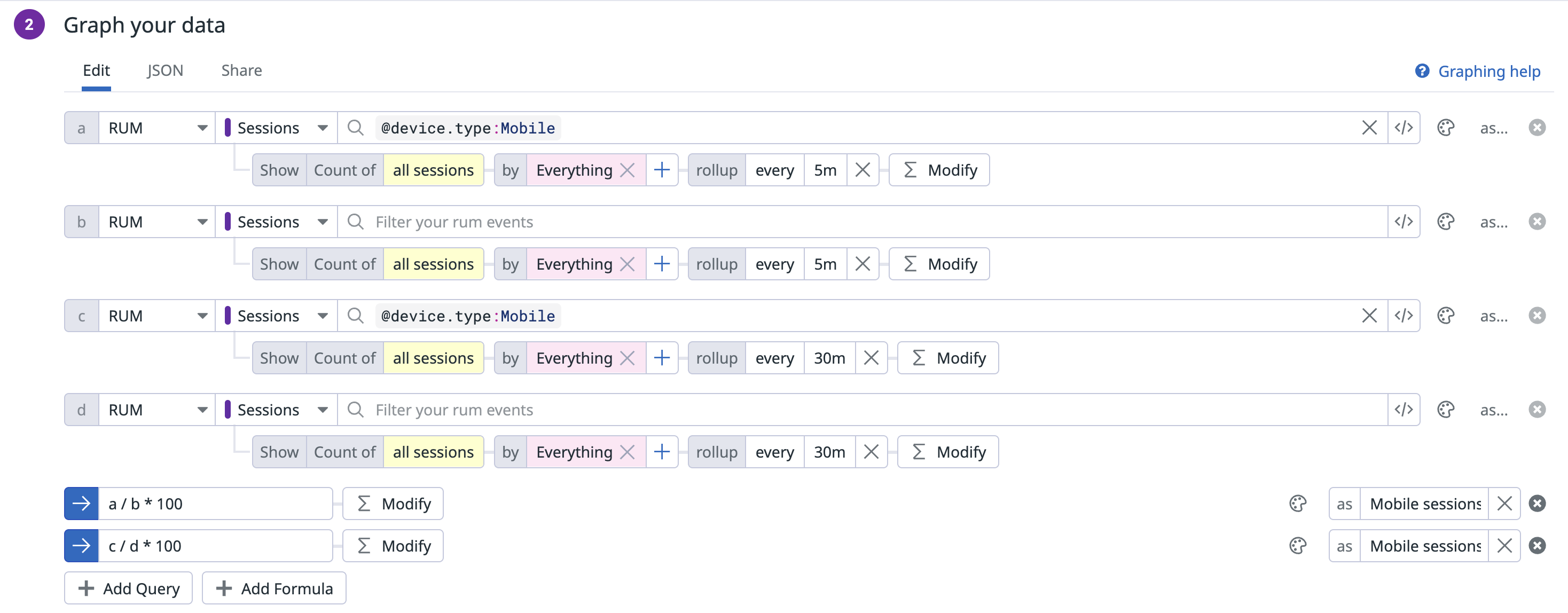
Configuration
Configuration
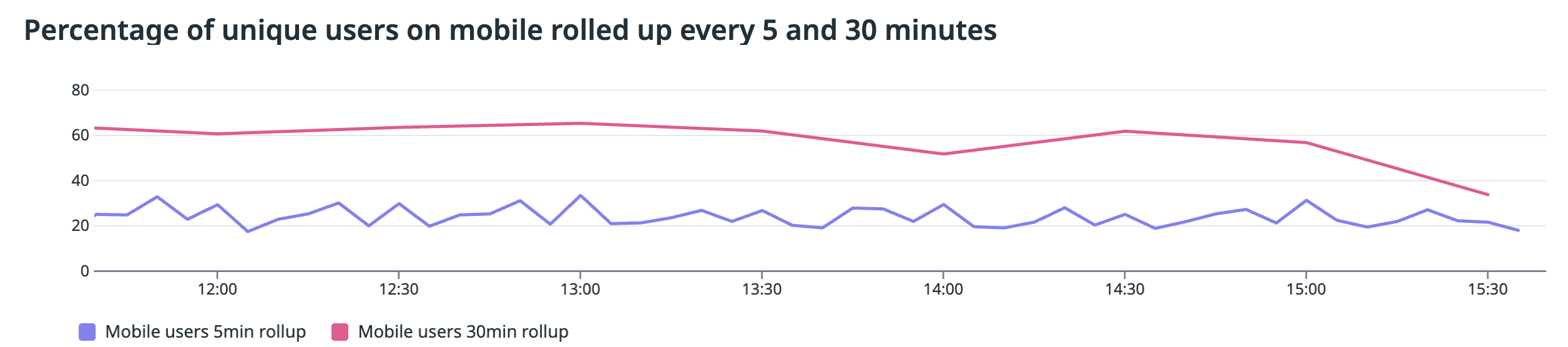
Cependant, lorsque vous regroupez par utilisateurs, les deux graphiques ne se superposent pas : le graphique de 30 minutes est significativement plus élevé que le graphique de 5 minutes. Cela peut ressembler à un bug au premier abord, mais cela montre en réalité comment les utilisateurs interagissent avec le service sur différentes périodes.
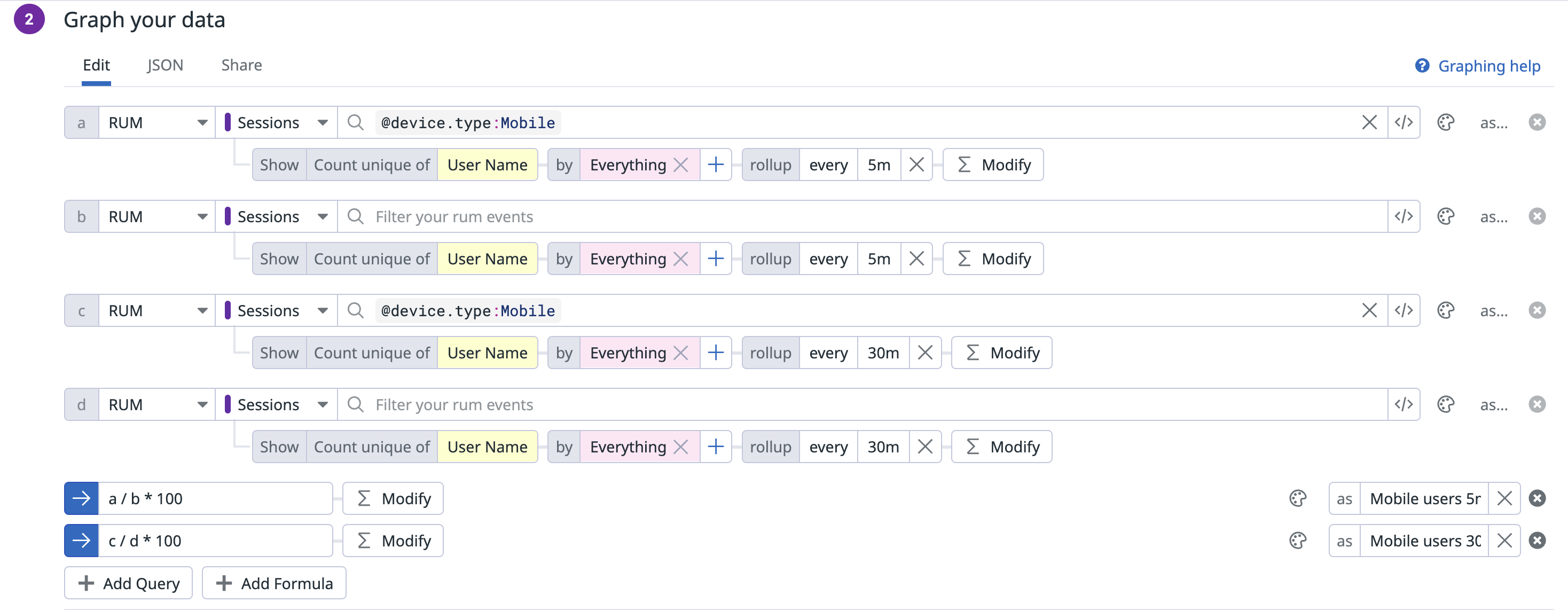
Configuration
Configuration
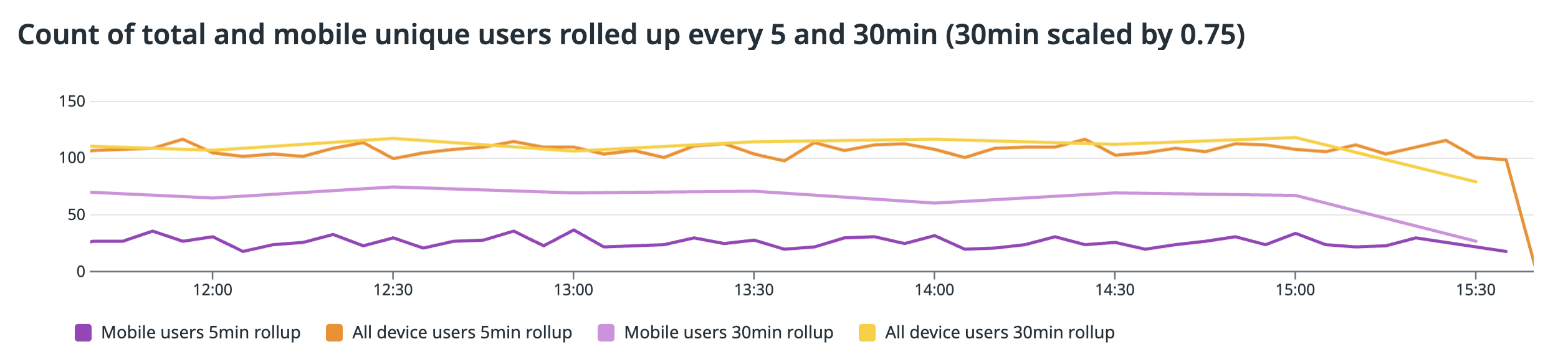
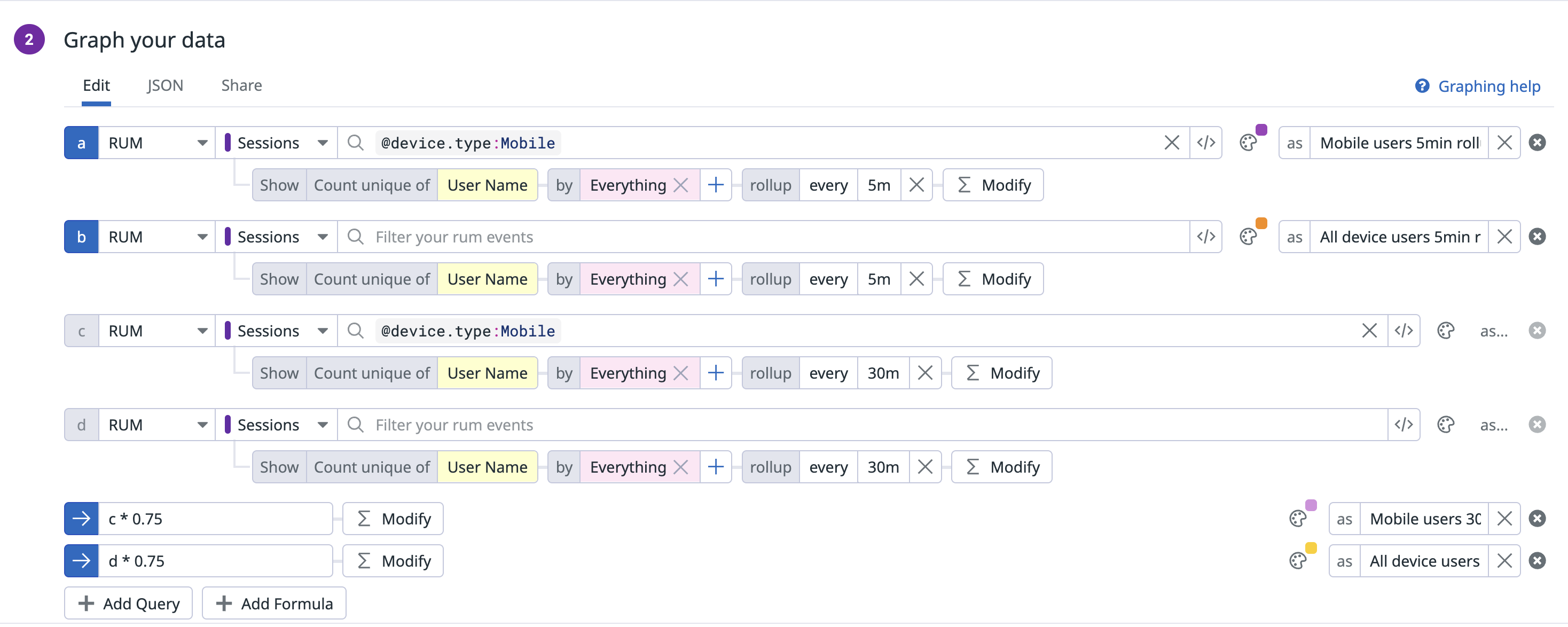
Le graphique suivant examine les rollups de 5 minutes par rapport à 30 minutes pour les utilisateurs distincts mobiles et les utilisateurs distincts totaux. Comme les rollups de 30 minutes sont naturellement plus grands que les rollups de 5 minutes, ce graphique affiche les rollups de 30 minutes réduits d’un facteur de 0,75. Pour les utilisateurs distincts totaux, les rollups de 5 minutes et de 30 minutes s’alignent approximativement. Cependant, pour les utilisateurs distincts mobiles, le rollup de 30 minutes est significativement plus élevé que le rollup de 5 minutes. Pourquoi ?
Configuration
Configuration
Cela se produit parce que lorsqu’un utilisateur apparaît plusieurs fois pendant une fenêtre de rollup, il apparaît une fois dans le dénominateur mais plusieurs fois dans le numérateur.
$$\text"cardinality:@usr.name[@type:session @device.type:Mobile]" / \text"cardinality:@usr.name[@type:session]" * 100$$
Une autre façon de comprendre cela est que lorsqu’un utilisateur apparaît plusieurs fois dans une fenêtre, chaque apparition représente une opportunité d’apparaître dans le numérateur. Dans une plage temporelle plus longue, chaque utilisateur apparaîtra plus de fois, créant plus d’opportunités de (dans ce cas) consulter la page sur mobile.
Pour illustrer cela concrètement, imaginez des utilisateurs qui consultent le site web sur des ordinateurs pendant la journée et ne consultent sur mobile que pendant le trajet du matin ou du soir. Si la moitié consulte pendant le trajet du matin, la moitié consulte pendant le trajet du soir et la moitié consulte pendant les deux (ce qui laisse un quart ne consultant pas du tout sur mobile) :
Un rollup de 12 heures vous montrerait 50 % des utilisateurs consultant sur mobile de minuit à midi (trajet du matin) et 50 % consultant de midi à minuit (trajet du soir).
Un rollup de 24 heures vous montrerait 75 % des utilisateurs consultant sur mobile (l’un ou l’autre trajet).
De même, un rollup d'1 heure pourrait vous montrer 10-20 % des utilisateurs consultant sur mobile pendant les heures de trajet, et <1 % pendant les heures hors trajet. C’est beaucoup plus petit que les plages temporelles plus grandes, mais toujours correct.
Pour aller plus loin
Documentation, liens et articles supplémentaires utiles: